© Projet Hévéa / CNRS Images. Licence CC BY-SA
Référence
20180083_0012
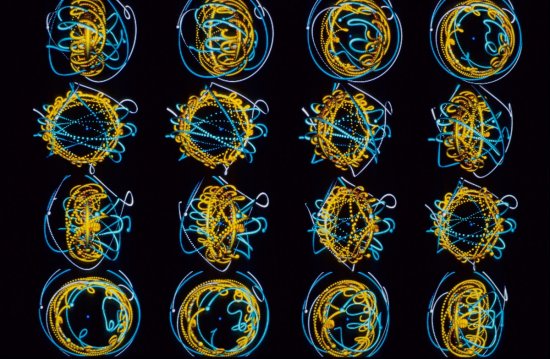
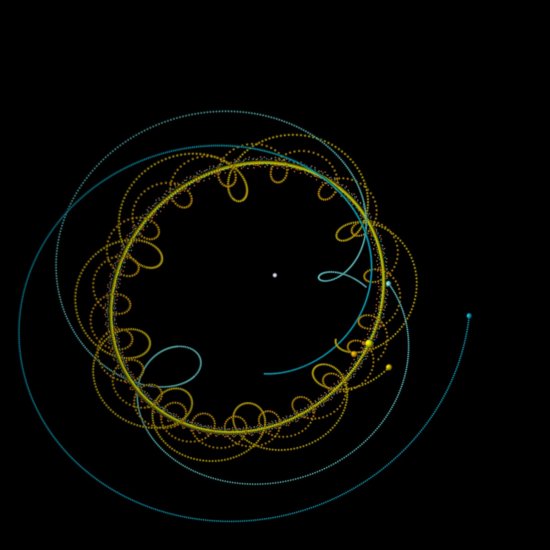
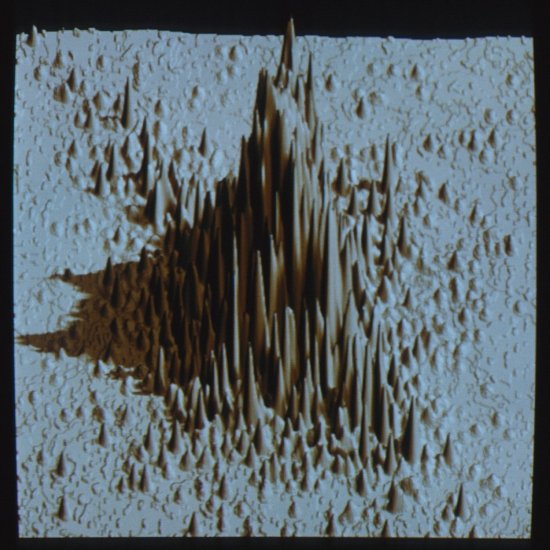
Détail d'une sphère réduite isométrique
Détail d'une sphère réduite isométrique. Cette surface paradoxale est isométrique à une sphère ronde : chaque point de la sphère réduite peut être mis en correspondance avec un point de la sphère ronde, de sorte que deux chemins quelconques se correspondant aient la même longueur. La réduction a été obtenue en rapprochant deux petites calottes extraites de la sphère ronde que l'on a jointes à l'aide d'une surface fortement déformée. Cette partie centrale présente une accumulation de corrugations (ondulations) dont l'amplitude croît à mesure que l'on s'écarte du bord des calottes. Un phénomène de transition analogue se retrouve dans la courbe de Koch, un exemple classique de courbe fractale.
L’utilisation des médias visibles sur la Plateforme CNRS Images peut être accordée sur demande. Toute reproduction ou représentation est interdite sans l'autorisation préalable de CNRS Images (sauf pour les ressources sous licence Creative Commons).
Aucune modification d'une image ne peut être effectuée sans l'accord préalable de CNRS Images.
Aucune utilisation à des fins publicitaires ou diffusion à un tiers d'une image ne peut être effectuée sans l'accord préalable de CNRS Images.
Pour plus de précisions consulter Nos conditions générales