© Stéphane DOUADY/CNRS Images
Référence
20050001_1599
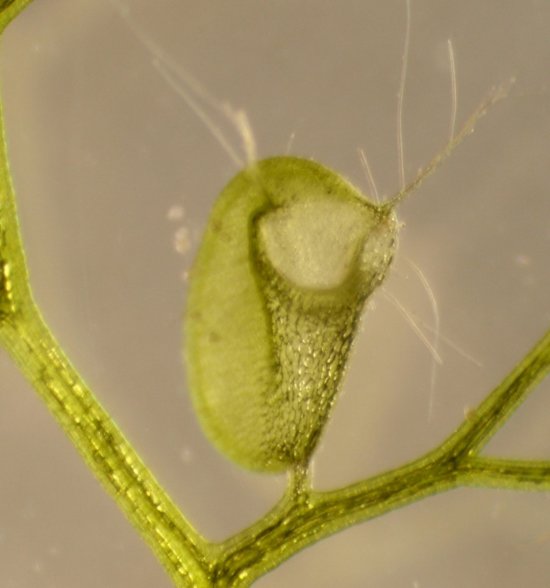
Chou Romanesco dont l'aspect fractal est quasiment parfait (un fractal est construit mathématiquemen
Chou Romanesco dont l'aspect fractal est quasiment parfait (un fractal est construit mathématiquement en dessinant une forme, et en la reproduisant à échelle plus petite plusieurs fois). Le cône central du choux est recouvert de spirales très régulières qui s'entrecroisent, partant du centre et s'agrandissant quand on s'éloigne vers la périphérie. À chaque croisement, le même motif de cône (recouvert de spirales) se reproduit. Et ainsi de suite... Le nombre de ces spirales est (presque) toujours des nombres consécutifs de la suite de Fibonacci, ici 8 et 13. L'objectif est de d'expliquer l'apparition du nombre d'or et de la suite de Fibonacci dans les plantes, plus généralement montrer l'importance de processus physiques et d'auto-organisation dans la morphogenèse.
L’utilisation des médias visibles sur la Plateforme CNRS Images peut être accordée sur demande. Toute reproduction ou représentation est interdite sans l'autorisation préalable de CNRS Images (sauf pour les ressources sous licence Creative Commons).
Aucune modification d'une image ne peut être effectuée sans l'accord préalable de CNRS Images.
Aucune utilisation à des fins publicitaires ou diffusion à un tiers d'une image ne peut être effectuée sans l'accord préalable de CNRS Images.
Pour plus de précisions consulter Nos conditions générales