© Vincent BLANLOEIL/CNRS Images
Reference
20080001_0796
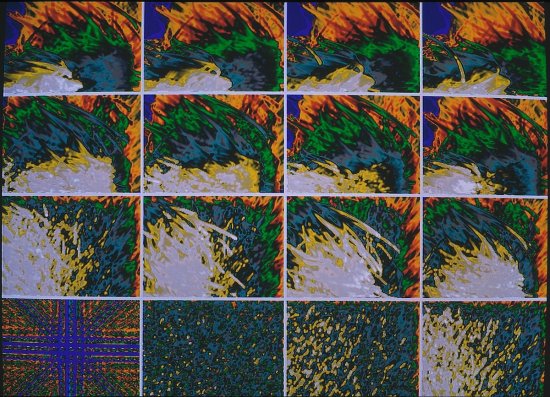
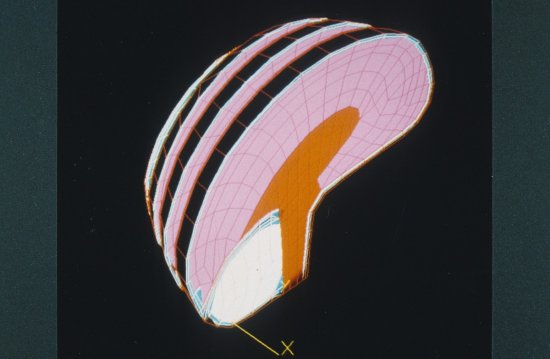
Modélisation de la sextique de Barth
Sextique de Barth. Cette image représente une surface algébrique définie par une équation polynomiale P (x, y, z) = 0, avec P de degré 6. La propriété remarquable de cette surface est de posséder 50 points doubles ordinaires. C'est à dire que la surface se coupe avec elle-même en exactement 50 points. C'est une forme particulière, d'une surface singulière de l'espace projectif complexe de dimension 3, définie par un polynôme de degré 6 et qui possède le maximum, pour ce degré, à savoir 65, de points doubles ordinaires possibles.
The use of media visible on the CNRS Images Platform can be granted on request. Any reproduction or representation is forbidden without prior authorization from CNRS Images (except for resources under Creative Commons license).
No modification of an image may be made without the prior consent of CNRS Images.
No use of an image for advertising purposes or distribution to a third party may be made without the prior agreement of CNRS Images.
For more information, please consult our general conditions